参考：

K条最短路径算法：Yen's Algorithm

算法背景

K 最短路径问题是最短路径问题的扩展和变形。1959 年，霍夫曼(Hoffman) 和帕夫雷(Pavley)在论文中第一次提出k 最短路径问题。 k 最短路径问题通常包括两类：有限制的k 最短路问题和无限制的K 最短路问题。 前者要求最短路径集合不含有回路，而后者对所求得的最短路径集合无限制。

算法简介

Yen's算法是Yen 在1971 年提出的以其名字命名 的Yen 算法。Yen's算法采用了递推法中的偏离路径算法思想，适用于非负权边的有向无环图结构。

算法思想

算法可分为两部分，算出第1条最短路径P(1)，然后在此基础上依次依次算出其他的K-1条最短路径。在求P(i+1) 时，将P(i)上除了终止节点外的所有节点都视为偏离节点，并计算每个偏离节点到终止节点的最短路径，再与之前的P(i)上起始节点到偏离节点的路径拼接，构成候选路径，进而求得最短偏离路径。

算法实例：

根据个人的理解，我归纳出了以下步骤：

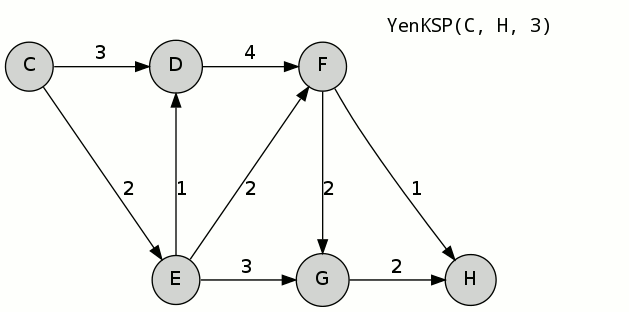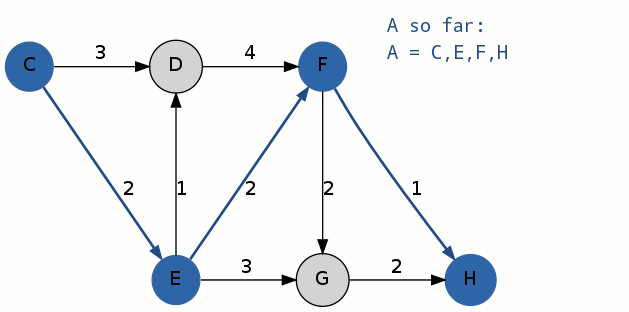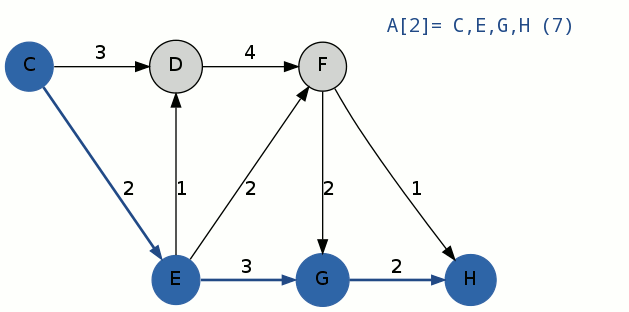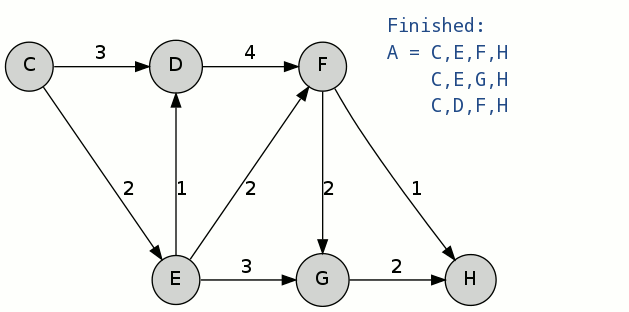
调用K条最短路径算法，源C，目的H，K为3。B为偏离路径集合。

1.通过Dijkstra算法计算得到最短路径A^1：C-E-F-H，其中，花费为5，A[1] = C-E-F-H；

2.将A[1]作为迭代路径，进行第一次迭代：

(1)以部分迭代路径(即A[1])C路径中，C点为起点，将C-E路径之间的权值设为无穷大，进行一次Dijkstra，得到路径A^2-1：C-D-F-H，花费为8，将A^2-1路径加入B；

(2)以部分迭代路径(即A[1])C-E路径中，E为起点，将E-F路径之间的权值设为无穷大，进行一次Dijkstra，得到路径A^2-2：C-E-G-H，花费为7，将A^2-2路径加入B；

(3)以部分迭代路径(即A[1])C-E-F路径中，F为起点，将F-H路径之间的权值设为无穷大，进行一次Dijkstra，得到路径A^2-3：C-E-F-G-H，花费为8，将A^2-3路径加入B；

迭代完成，B集合中有三条路径：C-D-F-H，C-E-G-H，C-E-F-G-H；选出花费最小的偏离路径C-E-G-H，A[2] = C-E-G-H，移出B集合。

3.将A[2]作为迭代路径，进行第二次迭代：

(1)以部分迭代路径(即A[2])C路径中，C点为起点，将C-E路径之间的权值设为无穷大，进行一次Dijkstra，得到路径A^3-1：C-D-F-H，但B集合已存在该路径，故不存在偏移路径；

(2)以部分迭代路径(即A[2])C-E路径中，E点为起点，将E-G、E-F路径之间的权值设为无穷大 (注意，这里设置两条路径的权值原因是这两条路径分别存在于A[1]和A[2]中)，进行一次Dijkstra，得到路径A^3-2：C-E-D-F-H，花费为8，将A^3-2加入B；

(3)以部分迭代路径(即A[2])C-E-G路径中，G点为起点，将C-H路径之间的权值设为无穷大，不存在偏移路径。

迭代完成，B集合中有三条路径：C-D-F-H，C-E-F-G-H，C-E-D-F-H；由于三条路径花费均为8，则根据最小节点数进行判断，选出偏离路径C-D-F-H，A[3] = C-D-F-H。

此时，选出了三条最短路径，分别是：

A[1] = C-E-F-HA[2] = C-E-G-HA[3] = C-D-F-H

算法结束。以上过程均为个人理解，如果出现了偏差，请大家指出，谢谢！

算法实现

可以参考Github中的一个使用python实现KSP算法的repo：

2017.8